Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
где:
π — математическая константа, она всегда равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Длина окружности
Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква π
(
пи
):
| C | = π . |
| D |
Таким образом, длину окружности (C
) можно вычислить, умножив константу
π
на диаметр (
D
), или умножив
π
на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно,
формула длины окружности будет выглядеть так:
C
=
πD
=
2πR
,
где C
— длина окружности,
π
— константа,
D
— диаметр окружности,
R
— радиус окружности.
Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
где:
π — математическая константа, равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Основные определения и свойства
| Фигура | Рисунок | Определения и свойства |
| Окружность | Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности | |
| Дуга | Часть окружности, расположенная между двумя точками окружности | |
| Круг | Конечная часть плоскости, ограниченная окружностью | |
| Сектор | Часть круга, ограниченная двумя радиусами | |
| Сегмент | Часть круга, ограниченная хордой | |
| Правильный многоугольник | Выпуклый многоугольник, у которого все стороны равны и все углы равны | |
| Около любого правильного многоугольника можно описать окружность |
| Окружность |
| Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности |
| Дуга |
| Часть окружности, расположенная между двумя точками окружности |
| Круг |
| Конечная часть плоскости, ограниченная окружностью |
| Сектор |
| Часть круга, ограниченная двумя радиусами |
| Сегмент |
| Часть круга, ограниченная хордой |
| Правильный многоугольник |
| Выпуклый многоугольник, у которого все стороны равны и все углы равны Около любого правильного многоугольника можно описать окружность |
Определение 1. Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
Рис.3
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Как определить диаметр трубы
Довольно часто возникает ситуация, когда дома нужно сделать небольшой ремонт. Например, заменить участок водопровода, системы отопления, канализации или трубы для подачи газа (что самостоятельно делается крайне редко, но все, же возможно теоретически).
Или же необходимо сделать новую систему водоснабжения, и для этого нужно точно определить диаметр старых труб, чтобы приобрести новые того же диаметра, но из другого материала. Или даже поручить ремонт мастерам, но для начала требуется приобрести трубу необходимого диаметра.
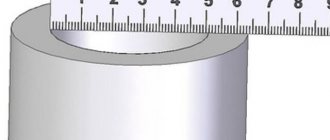
Конечно же, в продаже имеется много специализированных измерительных инструментов, позволяющих провести измерения быстро и точно. Например, линейки-циркометры или лазерные измерители. Но в мастерской домашнего мастера не всегда есть наготове такие специализированные высокоточные устройства. Поэтому возникает вопрос, как определить диаметр трубы подручными средствами?
Какие бывают диаметры и в чем они измеряются?
Прежде, чем переходить к измерениям, давайте немного вспомним, что диаметр трубы не обязательно указывается в сантиметрах. Исторически повелось, что часто трубные размеры обозначаются не в метрических (и привычных нам) сантиметрах, а в дюймах. Величина одного дюйма составляет 2,54 см.
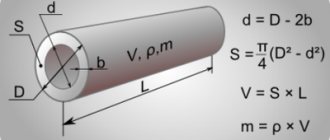
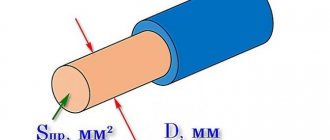
Кроме того, нужно учитывать, что у трубы есть два диаметра — наружный и внутренний. Внутренний диаметр определяет пропускную способность трубы (водопроводной, канализационной и так далее). Но наружный диаметр более важен при монтаже — именно по наружной стороне трубы наносится резьба, и по нему определяется резьбовое соединение.
Трубы из разного материала имеют различную толщину стенок, что определяет разницу между диаметрами наружным и внутренним.
Переходим к делу — ищем инструмент
Существует несколько различных способов измерения диаметра трубы. Для повышения точности измерения нужно прибегать к тому или иному способу, чтобы не допустить ошибки. Чаще всего условия выбора зависят от доступности самой трубы.
Самый распространенный и простой способ измерения — при помощи штангенциркуля. Но, во-первых, штангенциркуль есть не в каждом домашнем хозяйстве. А во-вторых, трубы большого диаметра (канализационные, например) не так просто замерить при помощи небольшого бытового измерителя. Но на помощь может прийти самый простой способ, не требующий сложных специализированных инструментов.
Для вычисления диаметра трубы потребуются:
- Гибкая линейка, портновский сантиметр или рулетка;
- Знание числа Пи (3,14);
- Калькулятор.
Измерить таким способом можно как трубу, так и любой другой предмет круглого сечения — колонну, пруток, садовую клумбу и так далее. Нужно выполнить только одно измерение – узнать длину окружности. Для этого следует обернуть трубу гибкой линейкой, сантиметром или рулеткой точно по окружности (если это клумба — то в самой широкой части). Затем разделить полученное значение на 3, 14 (любители точности могут разделить на 3, 1415926) и получить диаметр трубы в сантиметрах.
Для того чтобы перевести размеры в часто применяемые дюймы (для водопроводных труб), нужно умножить полученное значение на 0,398. И наоборот, чтобы перевести указанные в спецификациях (особенно, на трубах импортного производства) дюймы в сантиметры, диаметр в дюймах требуется умножить на 2,54.
Трубы малого диаметра — особенности измерения
Если нужно измерить диаметр тонкой трубы, то не нужно особо ничего выдумывать — проще всего диаметр измеряется обычным штангенциркулем. Единственное условие — это обеспечение доступа к трубе. И, конечно же, наличие самого штангенциркуля. Такой способ подходит для того, чтобы измерять доступные трубы не очень больших диаметров (до 150 мм).
Проще всего приложить штангенциркуль к торцу трубы, прижать его ножки к наружным стенкам и посмотреть на полученное значение. Оно и будет искомым диаметром.
Что делать, если труба недоступна?
Если подобраться к торцу трубы невозможно, (например, она является частью смонтированной системы), то ее диаметр тоже можно измерить штангенциркулем. Просто прижимать циркуль нужно не к торцу, а к боковой поверхности перпендикулярно к трубе. Кроме того, длина ножек измерительного прибора должна быть больше, чем половина диаметра измеряемой трубы.
Трубы большого диаметра
Основной способ измерения остается тот же, что упоминался раньше. При помощи рулетки или шнура определяется длина окружности. А затем, разделив полученную длину на 3,14 получаем искомый диаметр.
К примеру, если длина окружности составила 31,4 см, то диаметр трубы составляет 314 мм:3,14 = 100 мм.
Метод дистанционного измерения по фото
Эта не совсем стандартная методика определения диаметра используется, когда в наличии нет измерительного инструмента или к трубе невозможно с ним подобраться. В этом случае вопрос, как определить диаметр трубы решается при помощи мобильного телефона или фотоаппарата.
Для этого рядом с трубой располагают предмет всем известного размера (чаще всего — спичечный коробок, длина стенки которого составляет 50 мм, или монету). И фотографируют «инсталляцию» на мобильный телефон. Затем прямо на фотографии (или на экране компьютера) измеряют размеры трубы и известного предмета. Остается только перевести все цифры в реальный размер, пользуясь правилом пропорциональности.
Определение внутреннего диаметра трубы
Проще всего измерить внутренний диаметр трубы на срезе. Например, при помощи штангенциркуля, измерив, внутренний диаметр в максимальной точке. Иногда внутренний диаметр вычисляют, вычитая удвоенную толщину стенок из наружного диаметра.
Методы контроля параметров труб при производстве
В крупном производстве наружный диаметр толстых труб (для водопровода или канализации) также измеряется рулеткой.
Однако при этом используется более точная формула:
D = L:3,14 — 2∆p — 0,2 мм.
Диаметр (D) определяется с учетом удвоенной толщины полотна рулетки (∆p) и делается поправка на прилегание рулетки к стенке трубы, составляющую (из опытных данных) 0,2 мм. Учитывается при замере также величина допустимого отклонения. Например, для трубы диаметром 200 мм отклонение должно составлять не более 1,5 мм в любую сторону.
Чаще всего допустимые отклонения выражаются в процентах. Для изделий диаметром от 820 до 1020 мм отклонение должно составлять не более 7%. Для измерения труб такого диаметра в промышленных условиях применяются ультразвуковые измерители.
Толщина стенок в заводских условиях измеряется непосредственно, при помощи штангенциркуля. При этом величина отклонения толщины стенки от номинальной не должна превышать 5% (особенно в сторону уменьшения).
Кроме того, на производстве контролю подлежат такие параметры изделий, как кривизна и овальность.
- Кривизна (отклонение от прямой линии) не должна быть больше 1,5 мм на погонный метр, а общая кривизна не должна превышать 0,15% по отношению к общей длине.
- Овальность трубы (то есть отношение к номинальному диаметру разности наибольшего и наименьшего диаметров) не должна быть больше 0,8%-1%. Наибольший и наименьший диаметр можно получить, измерив нутромером внутренние диаметры в двух перпендикулярных плоскостях.
Однако если нужно просто измерить диаметр трубы для замены, то нужны в сложных вычислениях и высокоточных приборах нет. Получить значение диаметра трубы можно, применив подручные средства и знания из школьного курса математики.
Видео: КАК ИЗМЕРИТЬ ДИАМЕТР ТРУБЫ
Площадь круга
Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами радиусами 1 и R, в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.
Рис.1
Площадь правильного n – угольника, вписанного в окружность радиуса R, равна
Площадь правильного n – угольника, вписанного в окружность радиуса 1, равна
Следовательно,
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1, стремится к π, то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу πR2.
Таким образом, площадь круга радиуса R, обозначаемая S, равна
S = πR2.