How to find the circumference of a circle using the sides and area of an inscribed triangle
You can find the length of a circle if a triangle is inscribed in it and all three of its sides are known, and its area is also known:
Where:
π is a mathematical constant, it is always equal to 3.14
a is the first side of the triangle
b - second side of the triangle
c - third side of the triangle
S is the area of the triangle
Circumference
The length of any circle is greater than its diameter by the same number of times, namely approximately 3.14 times. To denote this quantity, the small (lowercase) Greek letter π
(
pi
):
| C | = π . |
| D |
Thus, the circumference ( C
) can be calculated by multiplying the constant
π
by the diameter (
D
), or by multiplying
π
by twice the radius, since the diameter is equal to two radii.
Therefore, the formula for circumference will look like this:
C
=
πD
=
2πR
,
where C
is the circumference,
π
is a constant,
D
is the diameter of the circle,
R
is the radius of the circle.
Since the circumference is the boundary of a circle, the circumference of a circle can also be called the length of a circle or the perimeter of a circle.
How to find the circumference of a circle using the area and semi-perimeter of a circumscribed triangle
You can determine what the circumference is if the circle is inscribed in a triangle, and the following parameters are known: the area of the triangle and its semi-perimeter.
The perimeter is the sum of all sides of the triangle. The semi-perimeter is half this amount, so to find it you need to calculate the perimeter and divide it by two.
Where:
π is a mathematical constant equal to 3.14
S is the area of the triangle
p is the semi-perimeter of the triangle
Basic definitions and properties
| Figure | Drawing | Definitions and properties |
| Circle | A set of points on a plane located at the same distance from one point - the center of the circle | |
| Arc | The part of a circle located between two points on the circle | |
| Circle | The final part of a plane bounded by a circle | |
| Sector | Part of a circle limited by two radii | |
| Segment | Part of a circle bounded by a chord | |
| Regular polygon | A convex polygon in which all sides are equal and all angles are equal | |
| Any regular polygon can be described as a circle |
| Circle |
| A set of points on a plane located at the same distance from one point - the center of the circle |
| Arc |
| The part of a circle located between two points on the circle |
| Circle |
| The final part of a plane bounded by a circle |
| Sector |
| Part of a circle limited by two radii |
| Segment |
| Part of a circle bounded by a chord |
| Regular polygon |
| A convex polygon in which all sides are equal and all angles are equal Any regular polygon can be described as a circle |
Definition 1. The area of a circle is the limit to which the areas of regular polygons inscribed in a circle tend when the number of sides increases indefinitely.
Definition 2. The circumference is the limit to which the perimeters of regular polygons inscribed in a circle tend, with an unlimited increase in the number of sides.
Remark 1. The proof that the limits of the areas and perimeters of regular polygons inscribed in a circle really exist with an unlimited increase in the number of sides goes beyond the scope of school mathematics and is not given in our reference book.
Definition 3. The number π (pi) is the number equal to the area of a circle of radius 1.
Remark 2. The number π is an irrational number, i.e. a number that is expressed as an infinite non-periodic decimal fraction:
The number π is a transcendental number, that is, a number that cannot be the root of an algebraic equation with integer coefficients.
Arc length
Consider the circular arc shown in Figure 3 and denote its length by the symbol L(α), where the letter α denotes the value of the corresponding central angle.
Fig.3
In the case where the value α is expressed in degrees, the proportion is valid
from which the equality follows:
In the case where the value α is expressed in radians, the proportion is valid
from which the equality follows:
How to determine pipe diameter
Quite often a situation arises when a small renovation needs to be done at home.
For example, replacing a section of the water supply system, heating system, sewerage system or gas supply pipe (which is extremely rarely done independently, but still theoretically possible). Or it is necessary to make a new water supply system, and for this you need to accurately determine the diameter of the old pipes in order to purchase new ones of the same diameter, but from a different material. Or even entrust the repair to specialists, but first you need to purchase a pipe of the required diameter.
Of course, there are many specialized measuring instruments on the market that allow you to take measurements quickly and accurately. For example, circometer rulers or laser meters. But the home craftsman’s workshop does not always have such specialized high-precision devices at the ready. Therefore, the question arises, how to determine the diameter of the pipe using improvised means?
What are the diameters and how are they measured?
Before moving on to measurements, let's remember a little that the diameter of the pipe is not necessarily indicated in centimeters. Historically, it has been the custom that pipe dimensions are often indicated not in metric (and familiar to us) centimeters, but in inches. The size of one inch is 2.54 cm.
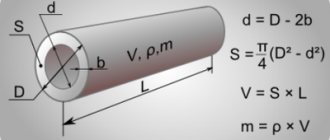
In addition, you need to take into account that the pipe has two diameters - outer and inner. The internal diameter determines the throughput of the pipe (water supply, sewer, etc.). But the outer diameter is more important during installation - it is on the outer side of the pipe that the thread is applied, and the threaded connection is determined from it.
Pipes made of different materials have different wall thicknesses, which determines the difference between the outer and inner diameters.
Let's get down to business - looking for a tool
There are several different ways to measure pipe diameter. To increase the accuracy of measurement, you need to resort to one method or another to prevent errors. Most often, the selection conditions depend on the availability of the pipe itself.
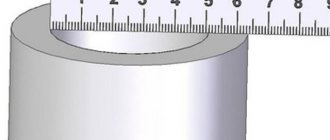
The most common and easiest way to measure is using a caliper. But, firstly, not every household has a caliper. And secondly, large-diameter pipes (sewage, for example) are not so easy to measure using a small household meter. But the simplest method that does not require complex specialized tools can come to the rescue.
To calculate the pipe diameter you will need:
- Flexible ruler, tailor's centimeter or tape measure;
- Knowledge of Pi number (3.14);
- Calculator.
In this way, you can measure both a pipe and any other object of round cross-section - a column, a rod, a garden bed, and so on. You only need to take one measurement - find out the circumference. To do this, wrap the pipe with a flexible ruler, centimeter or tape measure exactly around the circumference (if it is a flowerbed, then in the widest part). Then divide the resulting value by 3.14 (those who like precision can divide by 3.1415926) and get the pipe diameter in centimeters.
In order to convert dimensions to commonly used inches (for water pipes), you need to multiply the resulting value by 0.398. Conversely, to convert the inches indicated in the specifications (especially for imported pipes) into centimeters, the diameter in inches must be multiplied by 2.54.
Small diameter pipes - measurement features
If you need to measure the diameter of a thin pipe, then you don’t need to invent anything special - the easiest way is to measure the diameter with a regular caliper. The only condition is to ensure access to the pipe. And, of course, the presence of the caliper itself. This method is suitable for measuring accessible pipes of not very large diameters (up to 150 mm).
The easiest way is to attach a caliper to the end of the pipe, press its legs against the outer walls and look at the resulting value. This will be the required diameter.
What to do if the pipe is not accessible?
If it is impossible to get to the end of the pipe (for example, it is part of an installed system), then its diameter can also be measured with a caliper. You just need to press the compass not to the end, but to the side surface perpendicular to the pipe. In addition, the length of the legs of the measuring device must be greater than half the diameter of the pipe being measured.
Large diameter pipes
The basic measurement method remains the same as mentioned before. Using a tape measure or cord, determine the circumference. And then, dividing the resulting length by 3.14, we obtain the desired diameter.
For example, if the circumference is 31.4 cm, then the pipe diameter is 314 mm: 3.14 = 100 mm.
Photo remote sensing method
This not entirely standard method for determining the diameter is used when there is no measuring tool available or it is impossible to get close to the pipe with one. In this case, the question of how to determine the diameter of the pipe is solved using a mobile phone or camera.
To do this, an object of known size is placed next to the pipe (most often a matchbox with a wall length of 50 mm, or a coin). And they take pictures of the “installation” on a mobile phone. Then the dimensions of the pipe and the known object are measured directly on the photograph (or on the computer screen). All that remains is to convert all the numbers into real size, using the rule of proportionality.
Determining the internal diameter of a pipe
The easiest way is to measure the internal diameter of the pipe at the cut. For example, using a caliper, measuring the internal diameter at the maximum point. Sometimes the inside diameter is calculated by subtracting twice the wall thickness from the outside diameter.
Methods for monitoring pipe parameters during production
In large-scale production, the outer diameter of thick pipes (for water supply or sewerage) is also measured with a tape measure.
However, a more precise formula is used:
D = L:3.14 - 2∆p - 0.2 mm.
The diameter (D) is determined taking into account the double thickness of the tape measure (∆p) and a correction is made for the fit of the tape measure to the pipe wall, which is (from experimental data) 0.2 mm. The value of the permissible deviation is also taken into account when measuring. For example, for a pipe with a diameter of 200 mm, the deviation should be no more than 1.5 mm in any direction.
Most often, permissible deviations are expressed as percentages. For products with a diameter from 820 to 1020 mm, the deviation should be no more than 7%. To measure pipes of this diameter in industrial conditions, ultrasonic meters are used.
The wall thickness in the factory is measured directly using a caliper. In this case, the deviation of the wall thickness from the nominal one should not exceed 5% (especially in the decreasing direction).
In addition, such product parameters as curvature and ovality are subject to control in production.
- The curvature (deviation from a straight line) should not be more than 1.5 mm per linear meter, and the total curvature should not exceed 0.15% in relation to the total length.
- The ovality of the pipe (that is, the ratio of the difference between the largest and smallest diameters to the nominal diameter) should not be more than 0.8% -1%. The largest and smallest diameters can be obtained by measuring the internal diameters in two perpendicular planes with a bore gauge.
However, if you just need to measure the diameter of a pipe for replacement, then you don’t need complex calculations and high-precision instruments. You can obtain the value of the pipe diameter by using available tools and knowledge from a school mathematics course.
Video: HOW TO MEASURE THE PIPE DIAMETER
Area of a circle
Let's consider two circles with a common center (concentric circles) and radii of radii 1 and R, in each of which a regular n - square is inscribed (Fig. 1).
Let us denote by O the common center of these circles. Let the inner circle have radius 1.
Fig.1
The area of a regular n-gon inscribed in a circle of radius R is equal to
The area of a regular n-gon inscribed in a circle of radius 1 is equal to
Hence,
Since as n increases, the area of a regular n-gon inscribed in a circle of radius 1 tends to π, then as n increases, the area of a regular n-gon inscribed in a circle of radius R tends to the number πR2.
Thus, the area of a circle of radius R, denoted S, is
S = πR2.