Как закон Всемирного Тяготения Ньютона действовал задолго до самого Ньютона, так и уравнение Бернулли существовало задолго до того, как родился сам Бернулли. Ему удалось лишь облечь это уравнение в наглядную форму, в чем его неоспоримая и огромная заслуга. Зачем мне уравнение Бернулли, спросите Вы, ведь я прекрасно жил и без него. Да, но оно может пригодиться Вам хотя бы на экзамене по гидравлике! Как говорится, «все не так уж плохо, если ты знаешь и можешь сформулировать уравнение Бернулли».
Размеры
Диаметр
В случае водопроводных и газовых труб мы имеем дело с не вполне обычной системой измерений. Для соответствующих трубопроводов в качестве основного параметра используется несколько непривычное понятие условного прохода, или условного диаметра (ДУ). Он измеряется как в дюймах, так и в миллиметрах; одна и та же ВГП труба может продаваться как 1 1/4 дюйма или ДУ32 мм.
Справка: в качестве меры длины в этом случае используется британский дюйм, равный 2,54 сантиметра. При пересчете дюймов в миллиметры следует учитывать предусмотренный ГОСТ шаг условных диаметров; так, в приведенном выше случае простой пересчет 1 1/4 дюйма в миллиметры даст не 32, а 1,25х2,54=31,75 мм.
Приведем предусмотренные ГОСТ 3262-75 размеры водогазопроводных труб.
| Условный проход (ДУ), мм | Фактический наружный диаметр, мм |
| 15 | 21,3 |
| 20 | 26,8 |
| 25 | 33,5 |
| 32 | 42,3 |
| 40 | 48,0 |
| 50 | 60,0 |
| 65 | 75,5 |
| 80 | 88,5 |
| 90 | 101,3 |
| 100 | 114,0 |
| 125 | 140,0 |
| 150 | 165,0 |
Поскольку толщина стенок варьируется в пределах одного типоразмера (трубы производятся легкими, обыкновенными и усиленными), можно сказать, что ДУ в общем случае близок к внутреннему диаметру, но, как правило, не равен ему.
Условный проход близок к внутреннему диаметру трубы.
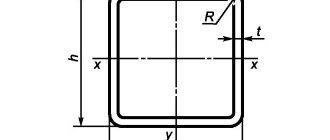
Сечение
При строительстве водопроводов используются, за редким исключением, трубы круглого сечения.
Тому есть две весьма веских причины.
- У круглой трубы минимальная площадь стенок при максимальной площади сечения. Стало быть, цена погонного метра трубопровода при фиксированной толщине стенки будет минимальной – просто из-за меньшего расхода материала.
- Круглое сечение обеспечивает максимальную прочность на разрыв. Дело в том, что сила, с которой внутренняя среда с избыточным давлением давит на стенки, прямо пропорциональна их площади; а площадь, как мы уже выяснили, минимальна именно у круглой трубы.
Магистрали высокого давления всегда имеют круглое сечение.
Площадь внутреннего сечения вычисляется по формуле S=Pi*R^2, где S – искомое значение площади, Pi – число “пи”, приблизительно равное 3,14159265, а R – радиус (половина внутреннего диаметра). Скажем, у трубы с внутренним диаметром 200 мм сечение будет равно 3,14159265х(0,1^2)=0,031 м2.
Поскольку течение жидкости в круглой трубе не всегда связано с заполнением всего ее объема, при расчетах нередко используется понятие “живого сечения”. Так называют площадь сечения потока. Скажем, при заполнении трубы ровно наполовину она будет равна (Pi*R^2)/2 (в приведенном выше примере – 0,031/2=0,00155 м2).
Живое сечение для напорной, самотечной канализации и для лотка.
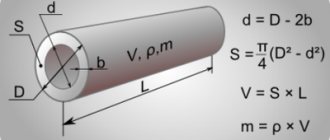
Объем
Давайте выясним, чему равен объем жидкости в трубе. С точки зрения геометрии любая труба представляет собой цилиндр. Его объем рассчитывается как произведение площади сечения и длины.
Так, при площади сечения 0,031 м2 объем жидкости в полностью заполненном трубопроводе длиной 8 метров будет равен 0,031х8=0,248 м3.
При частично заполненной трубе для расчета используется среднее живое сечение. При постоянном уклоне и расходе движение жидкости по трубам будет равномерным; соответственно, живое сечение будет одинаковым на всех участках безнапорного трубопровода.
Расход
Разберемся, как выглядит расчет расхода жидкости через трубу. Задача имеет большую практическую ценность: она непосредственно связана с расчетами водопроводов при известном количестве сантехнических приборов.
Должны огорчить вас: простой и универсальной методики расчета не существует. Почему?
Просто потому, что при выполнении полного гидродинамического расчета своими руками нужно учитывать огромный ряд факторов:
- Коэффициент трения внутренней поверхности трубы. Очевидно, что шероховатая, покрытая отложениями сталь будет оказывать движению воды куда большее сопротивление, чем гладкий полипропилен.
Снимок позволяет оценить зарастание стальной трубы.
- Длина трубопровода. Чем большее расстояние предстоит пройти жидкости, тем большим будет падение напора из-за торможения потока о стенки, тем сильнее уменьшится расход.
- Диаметр трубопровода влияет на течение вязкой жидкости по трубам куда более сложным образом, чем это может показаться. Чем меньше сечение, тем большее сопротивление труба оказывает потоку. Причина – в том, что с уменьшением диаметра изменяется соотношение ее внутреннего объема и площади стенок.
Обратите внимание! В толстом трубопроводе ближняя к стенкам часть потока выполняет роль своеобразной смазки для его внутренней части. В тонком же толщина слоя этой смазки оказывается недостаточной.
- Наконец, каждый поворот трубопровода, переход диаметра, каждый элемент запорной арматуры тоже влияет на расход жидкости в нем, тормозя поток.
Повороты и элементы запорной арматуры вызывают падение напора.
Нужно понимать, что все перечисленные факторы влияют на результат вовсе не на единицы процентов: скажем, для новой стальной трубы с полированной внутренней поверхностью и для заросшей отложениями (даже без учета падения просвета) гидродинамическое сопротивление отличается более чем в 200 раз.
Для профессионалов все необходимые для гидравлического расчета трубопровода с учетом его полной конфигурации, материала и возраста данные приводятся в таблицах Ф.А. Шевелева. На основе этих таблиц создано много онлайн-калькуляторов, позволяющих выполнить расчет с той или иной степенью достоверности.
Есть, однако, одна лазейка, позволяющая существенно упростить самостоятельные расчеты. При расходе жидкости через отверстие, пренебрежимо малое по сравнению с подводящей жидкость трубой (что, собственно, мы и наблюдаем при работе большинства сантехнических приборов), действует закон Торричелли.
Эванджелиста Торричелли, один из основоположников гидродинамики.
Согласно этому закону, в описанном случае действует формула V^2=2gH, где V – скорость потока в отверстии, g – ускорение свободного падения (9,78 м*с^2), а H – высота столба над отверстием или, что то же самое, напор перед ним.
Справка: 1 атмосфера (1 кгс/см2) соответствует напору водяного столба в 10 метров.
Как скорость потока в отверстии увязывается с расходом? В нашем случае инструкция по расчету проста: через отверстие с площадью сечения S пройдет объем жидкости, равный произведению S на скорость потока V.
Давайте в качестве примера рассчитаем расход воды через отверстие диаметром 2 сантиметра при напоре в 10 метров, соответствующем одной атмосфере избыточного давления.
- V^2=2 х 9,78*10 = 195,6
- V равно квадратному корню из 195,6. Результат (13,985706 м/с) для простоты расчетов округлим до 14 м/с.
- Площадь сечения отверстия с диаметром в два сантиметра согласно приведенной выше формуле равна 3,14159265*0,01^2=0,000314159265 м2.
- Расход, стало быть, будет равным 0,000314159265*14=0,00439822971 м3/с. Для удобства переведем его в литры: поскольку 1 кубометр равен 1000 литров, в сухом остатке будет результат в 4,4 литра в секунду.
Для полноты картины приведем некоторые справочные данные.
| Сантехнический прибор | Средний расход воды, л/с |
| Умывальник с водоразборным краном | 0,1 |
| Умывальник со смесителем | 0,12 |
| Мойка со смесителем | 0,12 |
| Ванна со смесителем | 0,25 |
| Биде со смесителем и аэратором | 0,08 |
| Сливной бачок унитаза | 0,1 |
| Посудомоечная машина (набор воды) | 0,3 |
| Автоматическая стиральная машина | 0,25 |
Заметьте: при последовательном подключении все задействованные приборы создают нагрузку на общую подводку.
Скорость потока
Как выглядит расчет скорости потока жидкости в трубе? В случае ее вытекания через отверстие небольшого диаметра действует приведенный выше закон Торричелли.
Однако в большинстве случаев скорость потока жидкости в трубе рассчитывается для трубопровода большой протяженности, гидравлическим сопротивлением которого нельзя пренебречь. Раз так – мы сталкиваемся с теми же проблемами: на скорость при постоянном перепаде на участке влияет слишком большое количество факторов.
Ситуация резко упрощается, если нам известен расход. Для несжимаемых жидкостей действует упрощенная формула уравнения непрерывности: Q=Av, где Q – расход воды в метрах в секунду, А – площадь полного или живого сечения, v – средняя скорость жидкости в трубе круглого сечения или любой другой формы.
Зная приведенные выше справочные данные расхода воды сантехприборами, нетрудно рассчитать скорость движения потока в водопроводной трубе известного диаметра.
В качестве примера давайте выясним, с какой скоростью будет двигаться вода в подводке ХВС с внутренним диаметром 15 мм (0,015 м) при одновременном наполнении сливного бачка, использовании посудомоечной машины и умывальника.
На фото – подводки водоснабжения в квартире. 15 мм – наиболее часто применяемый диаметр.
- Суммарный расход воды приборами, согласно приведенной выше таблице, составит 0,1 + 0,3 + 0,12 = 0,52 л/с, или 0,00052 м3/с.
- Площадь сечения трубы равна 3,14159265 х 0,0075 м^2 = 0,000176714865625 м2.
- Скорость потока в метрах в секунду равна 0,00052 / 0,000176714865625 = 2,96.
Для справки приведем некоторые значения скорости движения воды в трубопроводах различного назначения.
| Система | Диапазон скоростей, м/с |
| Самотечная система отопления | 0,2 – 0,5 |
| Система отопления с принудительной циркуляций, розлив | 0,5 – 3 |
| Система отопления с принудительной циркуляцией, подводки к отопительным приборам | 0,2 – 0,5 |
| Магистрали водоснабжения | 0,5 – 4 |
| Подводки водоснабжения | 0,5 – 1 |
| Циркуляция в системе ГВС | 0,2 – 0,5 |
| Безнапорная канализация (в том числе, ливневая канализация) | 0,35 – 1 |
Полезно: скорость потока до 1,5 м/с считается комфортной и не вызывающей ускорения абразивной эрозии стенок трубопровода. Приемлемо временное повышение скорости до 2,5 м/с.
Смысл уравнения Бернулли
Физический смысл уравнения Бернулли. Уравнение Бернулли является следствием закона сохранения энергии. Первый член уравнения Бернулли – это кинетическая энергия, второе слагаемое уравнения Бернулли – потенциальная энергия в поле силы тяжести, третье – работа силы давления при подъеме жидкости на высоту h.
Вот и все, друзья, не так уж и страшно. Совсем немного времени, а Вы уже знаете уравнение Бернулли. Даже если Вы не знаете больше ничего, с этими знаниями идти на экзамен или зачет гораздо лучше, чем просто так. А если Вам необходима помощь в том, как решать задачи на уравнение Бернулли – не стесняйтесь и оформляйте заявку. После того как наши авторы распишут решение уравнения Бернулли максимально подробно, у Вас не останется пробелов в знаниях.
Диаметр и давление
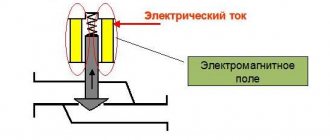
Еще один любопытный аспект поведения жидкости в трубе – взаимосвязь между скоростью потока и статическим давлением в нем. Она описывается законом Бернулли: статическое давление обратно пропорционально скорости потока.
Наглядная демонстрация действия закона.
Практическое применение этого закона нашло воплощение во многих современных механизмах.
Приведем лишь пару примеров:
- Пневматический краскопульт работает именно за счет создаваемого в струе воздуха разрежения, которое буквально высасывает краситель из бачка и превращает его в переносимый на окрашиваемую поверхность аэрозоль.
- В элеваторном узле дома, подключенного к теплотрассе, разрежение в создаваемой соплом струе воды из подающего трубопровода вовлекает через подсос часть воды из обратки в повторный цикл циркуляции.
Схема работы элеватора.
Кто такой Бернулли?
Даниил Бернулли – сын известного ученого Якоба Бернулли, швейцарский математик и физик. Жил с 1700 по 1782 годы, а с 1725 по 1733 трудился в Петербургской Академии наук. Помимо физики и математики Бернулли также изучал медицину наряду с Д’Аламбером и Эйлером считается отцом основателем математической физики. Успехи этого человека позволяют с уверенностью сказать, что это был настоящий «супермозг».
Д. Бернулли (1700-1782)