Just as Newton's law of universal gravitation was in effect long before Newton himself, so Bernoulli's equation existed long before Bernoulli himself was born. He only managed to put this equation into a visual form, which is his undeniable and enormous merit. Why do I need Bernoulli’s equation, you ask, because I lived just fine without it. Yes, but it may be useful to you at least for the hydraulics exam! As they say, “it’s not so bad if you know and can formulate Bernoulli’s equation.”
Dimensions
Diameter
In the case of water and gas pipes, we are dealing with a not entirely conventional measurement system. For the corresponding pipelines, the somewhat unusual concept of nominal bore, or nominal diameter (DN), is used as the main parameter. It is measured in both inches and millimeters; the same VGP pipe can be sold as 1 1/4 inches or DN32 mm.
Help: in this case, the British inch is used as a measure of length, equal to 2.54 centimeters. When converting inches into millimeters, the step of nominal diameters provided by GOST should be taken into account; So, in the above case, a simple conversion of 1 1/4 inches into millimeters will give not 32, but 1.25x2.54 = 31.75 mm.
Let us give the dimensions of water and gas pipes provided for by GOST 3262-75.
| Conditional bore (DN), mm | Actual outer diameter, mm |
| 15 | 21,3 |
| 20 | 26,8 |
| 25 | 33,5 |
| 32 | 42,3 |
| 40 | 48,0 |
| 50 | 60,0 |
| 65 | 75,5 |
| 80 | 88,5 |
| 90 | 101,3 |
| 100 | 114,0 |
| 125 | 140,0 |
| 150 | 165,0 |
Since the wall thickness varies within one standard size (pipes are produced in light, ordinary and reinforced), we can say that the diameter is generally close to the internal diameter, but, as a rule, is not equal to it.
The nominal bore is close to the internal diameter of the pipe.
Section
In the construction of water pipelines, with rare exceptions, round pipes are used.
There are two very good reasons for this.
- A round pipe has a minimum wall area with a maximum cross-sectional area . Therefore, the price per linear meter of pipeline with a fixed wall thickness will be minimal - simply due to lower material consumption.
- The round cross section provides maximum tensile strength . The fact is that the force with which the internal environment with excess pressure presses on the walls is directly proportional to their area; and the area, as we have already found out, is minimal for a round pipe.
High pressure lines always have a round cross-section.
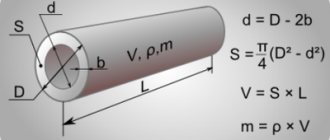
The internal cross-sectional area is calculated by the formula S=Pi*R^2, where S is the desired area value, Pi is the number “pi”, approximately equal to 3.14159265, and R is the radius (half the internal diameter). Let's say that a pipe with an internal diameter of 200 mm will have a cross-section equal to 3.14159265x(0.1^2)=0.031 m2.
Since the flow of liquid in a round pipe is not always associated with filling its entire volume, the concept of “real cross-section” is often used in calculations. This is the cross-sectional area of the flow. Let's say, when the pipe is filled exactly halfway, it will be equal to (Pi*R^2)/2 (in the example above - 0.031/2=0.00155 m2).
Living section for pressure, gravity sewerage and for a tray.
Volume
Let's find out what the volume of liquid in the pipe is. From a geometric point of view, any pipe is a cylinder. Its volume is calculated as the product of the cross-sectional area and length.
So, with a cross-sectional area of 0.031 m2, the volume of liquid in a completely filled pipeline 8 meters long will be equal to 0.031x8 = 0.248 m3.
When the pipe is partially filled, the average free cross-section is used for calculations. At a constant slope and flow rate, the movement of liquid through the pipes will be uniform; accordingly, the live cross-section will be the same in all sections of the free-flow pipeline.
Consumption
Let's figure out what the calculation of fluid flow through a pipe looks like. The problem has great practical value: it is directly related to the calculations of water supply systems with a known number of plumbing fixtures.
We must disappoint you: there is no simple and universal calculation method. Why?
Simply because when performing a complete hydrodynamic calculation with your own hands, you need to take into account a huge number of factors:
- Friction coefficient of the inner surface of the pipe. Obviously, rough, deposit-covered steel will offer much greater resistance to water movement than smooth polypropylene.
The image allows you to evaluate the overgrowth of a steel pipe.
- Pipeline length. The greater the distance the liquid has to travel, the greater the pressure drop will be due to flow deceleration against the walls, the more the flow rate will decrease.
- The diameter of the pipeline affects the flow of viscous fluid through the pipes in a much more complex way than it might seem. The smaller the cross-section, the greater the resistance the pipe has to the flow. The reason is that with a decrease in diameter, the ratio of its internal volume and wall area changes.
Note! In a thick pipeline, the part of the flow closest to the walls acts as a kind of lubricant for its internal part. In thin ones, the thickness of the layer of this lubricant is insufficient.
- Finally, every turn of the pipeline, change in diameter, every element of shut-off valves also affects the flow of liquid in it, slowing down the flow.
Turns and elements of shut-off valves cause a drop in pressure.
You need to understand that all of the above factors influence the result by more than a few percent: say, for a new steel pipe with a polished inner surface and for one overgrown with sediment (even without taking into account the drop in clearance), the hydrodynamic resistance differs by more than 200 times.
For professionals, all the data necessary for the hydraulic calculation of the pipeline, taking into account its full configuration, material and age, is given in the tables of F.A. Sheveleva. Based on these tables, many online calculators have been created that allow you to perform calculations with varying degrees of reliability.
There is, however, one loophole that can significantly simplify independent calculations. When the flow of liquid through a hole is negligible compared to the pipe supplying liquid (which, in fact, is what we observe in the operation of most plumbing fixtures), Torricelli’s law applies.
Evangelista Torricelli, one of the founders of hydrodynamics.
According to this law, in the described case the formula V^2=2gH applies, where V is the flow velocity in the hole, g is the acceleration of gravity (9.78 m*s^2), and H is the height of the column above the hole or something the same thing, the pressure in front of him.
Reference: 1 atmosphere (1 kgf/cm2) corresponds to a pressure of a water column of 10 meters.
How does the flow rate at the orifice relate to the flow rate? In our case, the calculation instructions are simple: a volume of liquid equal to the product of S and the flow velocity V will pass through a hole with cross-sectional area S.
As an example, let's calculate the water flow through a hole with a diameter of 2 centimeters at a head of 10 meters, corresponding to one atmosphere of excess pressure.
- V^2=2 x 9.78*10 = 195.6
- V is equal to the square root of 195.6. For ease of calculation, let’s round the result (13.985706 m/s) to 14 m/s.
- The cross-sectional area of a hole with a diameter of two centimeters according to the above formula is 3.14159265*0.01^2=0.000314159265 m2.
- The flow rate, therefore, will be equal to 0.000314159265*14=0.00439822971 m3/s. For convenience, let's convert it to liters: since 1 cubic meter is equal to 1000 liters, the bottom line will be 4.4 liters per second.
To complete the picture, we provide some background information.
| Plumbing fixture | Average water consumption, l/s |
| Washbasin with water tap | 0,1 |
| Washbasin with mixer tap | 0,12 |
| Sink with mixer | 0,12 |
| Bathtub with mixer | 0,25 |
| Bidet with mixer and aerator | 0,08 |
| Toilet cistern | 0,1 |
| Dishwasher (water set) | 0,3 |
| Automatic washing machine | 0,25 |
Please note: when connected in series, all devices involved create a load on the common supply.
Flow rate
What does it look like to calculate the speed of fluid flow in a pipe? If it flows out through a hole of small diameter, the above Torricelli law applies.
However, in most cases, the fluid flow rate in a pipe is calculated for a long pipeline, the hydraulic resistance of which cannot be neglected. If so, we are faced with the same problems: the speed with a constant difference in the area is influenced by too many factors.
The situation becomes dramatically simpler if we know the flow rate. For incompressible fluids, a simplified formula for the continuity equation applies: Q = Av, where Q is the water flow rate in meters per second, A is the total or live cross-sectional area, v is the average fluid velocity in a pipe of circular cross-section or any other shape.
Knowing the above reference data for water consumption by plumbing fixtures, it is not difficult to calculate the speed of flow in a water pipe of a known diameter.
As an example, let's find out at what speed water will move in a cold water line with an internal diameter of 15 mm (0.015 m) while simultaneously filling the drain tank and using a dishwasher and washbasin.
The photo shows water supply connections in the apartment. 15 mm is the most commonly used diameter.
- The total water consumption of the devices, according to the table above, will be 0.1 + 0.3 + 0.12 = 0.52 l/s, or 0.00052 m3/s.
- The cross-sectional area of the pipe is 3.14159265 x 0.0075 m^2 = 0.000176714865625 m2.
- The flow rate in meters per second is 0.00052 / 0.000176714865625 = 2.96.
For reference, we present some values of the speed of water movement in pipelines for various purposes.
| System | Speed range, m/s |
| Gravity heating system | 0,2 – 0,5 |
| Heating system with forced circulation, filling | 0,5 – 3 |
| Heating system with forced circulation, connections to heating devices | 0,2 – 0,5 |
| Water supply mains | 0,5 – 4 |
| Water supply connections | 0,5 – 1 |
| Circulation in the DHW system | 0,2 – 0,5 |
| Non-pressure sewerage (including storm sewerage) | 0,35 – 1 |
Useful: flow speeds of up to 1.5 m/s are considered comfortable and do not cause acceleration of abrasive erosion of the pipeline walls. A temporary increase in speed to 2.5 m/s is acceptable.
The meaning of Bernoulli's equation
Physical meaning of Bernoulli's equation. Bernoulli's equation is a consequence of the law of conservation of energy. The first term of the Bernoulli equation is kinetic energy, the second term of the Bernoulli equation is the potential energy in the gravitational field, the third is the work of the pressure force when the liquid rises to a height h.
That's it, friends, it's not so scary. Just a little time, and you already know the Bernoulli equation. Even if you don’t know anything else, going to an exam or test with this knowledge is much better than just doing it. And if you need help on how to solve problems using the Bernoulli equation, don’t hesitate to fill out a request. After our authors describe the solution to the Bernoulli equation in as much detail as possible, you will have no gaps in your knowledge.
Diameter and pressure
Another interesting aspect of the behavior of fluid in a pipe is the relationship between the flow rate and the static pressure in it. It is described by Bernoulli's law: static pressure is inversely proportional to flow velocity.
A clear demonstration of the law.
The practical application of this law is embodied in many modern mechanisms.
Let's give just a couple of examples:
- A pneumatic spray gun works precisely due to the vacuum created in the air stream, which literally sucks the dye out of the tank and turns it into an aerosol transferred to the surface to be painted.
- In the elevator unit of a house connected to the heating main, the vacuum in the jet of water created by the nozzle from the supply pipeline draws part of the water from the return into the repeated circulation cycle through suction.
Elevator operation diagram.
Who is Bernoulli?
Daniel Bernoulli is the son of the famous scientist Jacob Bernoulli, a Swiss mathematician and physicist. He lived from 1700 to 1782, and from 1725 to 1733 he worked at the St. Petersburg Academy of Sciences. In addition to physics and mathematics, Bernoulli also studied medicine along with D'Alembert and Euler, considered the founding father of mathematical physics. The success of this man allows us to say with confidence that he was a real “superbrain.”
D. Bernoulli (1700-1782)